前端算法之二叉树(1)

二叉树

1.平衡二叉树：任意一个节点其左节点的层数与右节点的层数相差不超过一
2.完全二叉树：除了叶子节点 之外每个节点都有两个子节点
3.满二叉树：
（1） 所有层都是满的
（2） 要么没有子节点，有子节点就必须要有两个

eg:平衡二叉树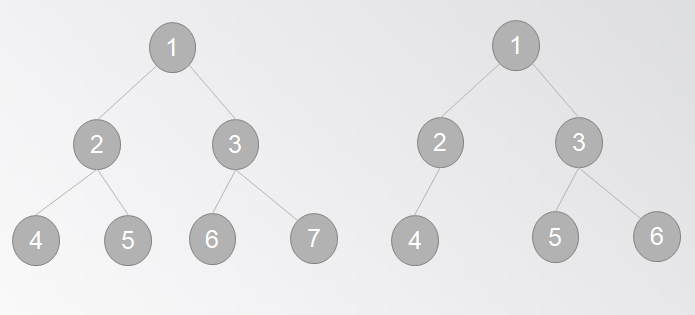

eg:完全二叉树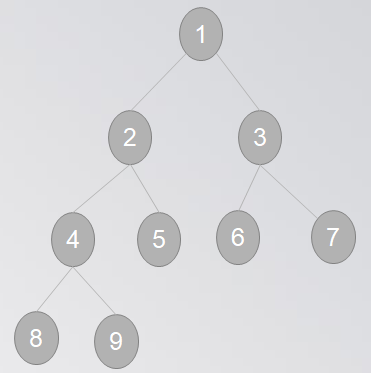

eg:满二叉树

二叉树的描述方式

1.前序：首先访问根节点 （ 根-> 左 -> 右）
2.中序： 中间访问根节点（ 左-> 根 -> 右）
3.后序： 最后访问根节点 ( 左-> 右 -> 根）

代码构造二叉树

1.菜鸟写法

function Node(data, left, right) {
          this.data = data;
          this.left = left;
          this.right = right;
      }
      function setTree() {
          var root = new Node(1, null, null);
          var node1 = new Node(2, null, null);
          var node2 = new Node(3, null, null);
          var node3 = new Node(4, null, null);
          var node4 = new Node(5, null, null);
          var node5 = new Node(6, null, null);
          var node6 = new Node(7, null, null);
          root.left = node1;
          root.right = node2;
          node1.left = node3;
          node1.right = node4;
          node2.left = node5;
          node2.right = node6;
          return root;
      }
      var tree = setTree();

这样写确实通俗易懂，但是实现起来所占空间实在是不敢恭维，所以我们是不是有什么办法，用更少的空间存储二叉树呢

2.进阶写法

function pre(node) {            //传入一棵树
          if (node == null) {
              return ;
          }
          pre(node.left);    //  使用递归  pre(node.left)->打印node.left的data值
          pre(node.right);   //  现在所看到的这个程序执行  左->右->根  的顺序，后序遍历
          console.log(node.data);
      }
pre(tree);

根据前序/中序遍历、后序/中序遍历确定一棵二叉树

为了方便，我们先把三种遍历方式的顺序写出来

var pre = [1,2,4,5,3,6];  //前序
var mid = [4,2,5,1,3,6];  //中序
var aft = [4,5,2,6,3,1];  //后序

1.前序/中序遍历

function perMid(pre, mid) {
           if(pre.length == 0 || mid.length == 0) {
               return null;
           }
           if (pre.length != mid.length) {
               throw Error('参数不正确')
           }
           // 根节点数据
           var rootData = pre[0];
           // 根节点在中序遍历中的位置
           var midRootIndex = mid.indexOf(rootData);
           // 左子树中序遍历
           var leftMid = mid.slice(0, midRootIndex);    //截取中序数组根节点之前的为左子树
           // 右子树中序遍历
           var rightMid = mid.slice(midRootIndex + 1);    //截取中序数组根节点之后的为右子树
           // 左子树前序遍历
           var leftPre = pre.slice(1, leftMid.length + 1);    /*截取前序数组：第一项是根节点所以从第二项开始截取，截取长度为左子树节点个数
                                                              所以截取到leftMid.length + 1的位置(slice不含下标为leftMid.length + 1)*/
            // 右子树前序遍历
           var rightPre = pre.slice(leftMid.length + 1);    //从leftMid.length + 1的位置开始截取，到最后
           // 左子树还原
           var left = perMid(leftPre, leftMid);    //递归，传入左子树的前、中序遍历
           // 右子树还原
           var right = perMid(rightPre, rightMid);    //同上
           
           // 最终二叉树
           var node = new Node(pre[0], left, right);
           return node;
       }

2.后序/中序遍历

function afterMid(aft, mid) {
          if(aft.length == 0 || mid.length == 0) {
              return null;
          }
          if (aft.length != mid.length) {
              throw Error('参数不正确')
          }
          // 根节点数据
          var rootData = aft[aft.length - 1];
          // 根节点在中序遍历中的位置
          var midRootIndex = mid.indexOf(rootData);
          // 左子树中序遍历
          var leftMid = mid.slice(0, midRootIndex);
          // 右子树中序遍历
          var rightMid = mid.slice(midRootIndex + 1);
          // 左子树后序遍历
          var leftAft = aft.slice(0, leftMid.length);
           // 右子树后序遍历
          var rightaft = aft.slice(leftMid.length, aft.length - 1);
          // 左子树还原
          var left = afterMid(leftAft, leftMid);
          // 右子树还原
          var right = afterMid(rightaft, rightMid);
          
          // 最终二叉树
          var node = new Node(aft[aft.length - 1], left, right);
          return node;
      }